Introduction
Dans le monde des jeux de mots, existent les anagrammes. Il s'agit de couples de mots utilisant les mêmes lettres. Par exemple CASSER et SACRES. Chaque lettre est utilisée le même nombre de fois mais la signification du mot est bien évidemment différente. Une version plus avancée des anagrammes est constituée des palindromes. Ils s'agit de mots qui se lisent à l'endroit et à l'envers et qui ont le même sens (comme KAYAK). Entre ces deux types de mots se trouvent les anacycliques. Il s'agit de couple de mots qui utilisent les mêmes lettres mais qui n'ont pas le même sens selon qu'on les lise à l'endroit où à l'envers. Par exemple NOEL et LEON ou bien TRACE et ECART sont des anacycliques. Les anacycliques font donc eux aussi partie de la famille des anagrammes avec la condition supplémentaire que l'ordre des lettres doit être inversé (et non pas seulement mélangé).
Pour en revenir aux nombres, on constate évidemment que tous les nombres sont anacycliques par définition. Par exemple 123 et 321. Quand on lit un nombre en sens inverse du sens de lecture on obtient forcément un autre nombre qui a une signification. L’intérêt ne réside donc pas là. La subtilité des nombres anacycliques consiste à prendre un nombre dans une base (traditionnellement en base 10) et de l'exprimer ensuite dans une autre base (par exemple en base 16).
L'exemple classique est le nombre 53 (en base 10) qui s'écrit 35 en base 16. C'est donc un nombre anacyclique. Le problème consiste donc à trouver tous les nombres anacycliques. Hélas, il ne semble pas y avoir d'autre solution que de tester de manière exhaustive tous les nombres en base 10 un à un afin de vérifier si ils sont anacycliques. En effet, un nombre anacyclique (comme 834 qui s’écrit 438 en base 14). Cela signifie que l'on a l'égalité suivante:

Ce qui peut aussi s'écrire sous la forme :
+3(10^1-14^1)+4(10^0-14^2)&space;=&space;0)
On en conclura qu'un nombre en base b de la forme a2a1a0 en base 10 (ici a2=8, a1=3, a0=4) est anacyclique si il est solution de l'équation suivante :
+a_1(10^1-14^1)+a_0(10^0-14^2)&space;=&space;0)
Et donc par extension que tout nombre anacyclique de longueur n doit résoudre l'équation suivante:
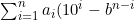=0)
Où b est la base dans laquelle on effectue le calcul. On obtient donc une équation à n inconnues (il faut trouver les différentes valeurs de ai). Attention cependant, il existe des nombres qui sont solution de cette équation mais qui ne sont pas anacycliques. Par contre si un nombre ne résout pas cette équation, on a la certitude qu'il n'est pas anacyclique.
Par exemple 13 (qui vaut 31 en base 4 et est donc un nombre anacyclique) est solution de cette équation mais 26 est aussi une solution (tout comme 39) alors que ces nombres ne sont pas anacycliques.
Malgré tout, nous voilà bien avancés puisqu'il faut tester toutes les combinaisons pour savoir si elles résolvent cette équation. Cependant, il ne sera pas obligatoire de tester tous les nombres de 1 à l'infini afin de trouver toutes les solutions.
Il est donc possible de trouver la limite haute des valeurs à tester pour chaque base. Le tableau suivant indique pour chaque base, le nombre de chiffres nécessaire pour écrire des nombres en base 10. Par exemple la troisième ligne du tableau correspond aux nombres à 3 chiffres en base 10 (c'est à dire les nombres de 100 à 999). Le tableau indique qu'en base 2, il faut entre 7 et 10 chiffres pour représenter ces nombres (en effet 100 s'écrit 1100100 et 999 s'écrit 1111100111). Ce qui rend impossible l'existence d'anacycliques dans cet intervalle. C'est pourquoi la case est colorée en bleu. Cela indique qu'il faut trop de chiffres pour espérer représenter ces nombres. De l'autre coté, en orange, se trouvent les cas où il faut moins de chiffres en base 10 que dans l'autre base, pour représenter les nombres. Il ne reste plus alors qu'à se limiter aux cases grises qui, elles, contiennent (au moins partiellement) des nombres ayant la même quantité de chiffres dans les deux bases (ce qui les rend éligibles au fait d'être anacycliques)
Ce qui peut aussi s'écrire sous la forme :
On en conclura qu'un nombre en base b de la forme a2a1a0 en base 10 (ici a2=8, a1=3, a0=4) est anacyclique si il est solution de l'équation suivante :
Et donc par extension que tout nombre anacyclique de longueur n doit résoudre l'équation suivante:
Où b est la base dans laquelle on effectue le calcul. On obtient donc une équation à n inconnues (il faut trouver les différentes valeurs de ai). Attention cependant, il existe des nombres qui sont solution de cette équation mais qui ne sont pas anacycliques. Par contre si un nombre ne résout pas cette équation, on a la certitude qu'il n'est pas anacyclique.
Par exemple 13 (qui vaut 31 en base 4 et est donc un nombre anacyclique) est solution de cette équation mais 26 est aussi une solution (tout comme 39) alors que ces nombres ne sont pas anacycliques.
Malgré tout, nous voilà bien avancés puisqu'il faut tester toutes les combinaisons pour savoir si elles résolvent cette équation. Cependant, il ne sera pas obligatoire de tester tous les nombres de 1 à l'infini afin de trouver toutes les solutions.
Réduction de l'espace de recherche
En effet, il est possible de réduire l'espace de recherche puisque l'une des règles d'un nombre anacyclique est qu'il doit forcement avoir le même nombre de chiffre. Or, plus la base est petite (par exemple en binaire), plus le nombre de chiffres nécessaire pour représenter un nombre est grand. Par exemple en base 10, le nombre 99 s'écrit avec 2 chiffres. Mais en base 2, il s'écrit avec avec 9 chiffres : 1100011. Il est donc forcement impossible de trouver des anacycliques en base deux avec des nombres élevés, uniquement parce que le nombre de chiffres nécessaires pour les écrire n'est pas le même (il n'est donc même pas nécessaire de tester si la lecture dans un sens en base 10 correspond à la lecture dans l'autre sens en base 2)Il est donc possible de trouver la limite haute des valeurs à tester pour chaque base. Le tableau suivant indique pour chaque base, le nombre de chiffres nécessaire pour écrire des nombres en base 10. Par exemple la troisième ligne du tableau correspond aux nombres à 3 chiffres en base 10 (c'est à dire les nombres de 100 à 999). Le tableau indique qu'en base 2, il faut entre 7 et 10 chiffres pour représenter ces nombres (en effet 100 s'écrit 1100100 et 999 s'écrit 1111100111). Ce qui rend impossible l'existence d'anacycliques dans cet intervalle. C'est pourquoi la case est colorée en bleu. Cela indique qu'il faut trop de chiffres pour espérer représenter ces nombres. De l'autre coté, en orange, se trouvent les cas où il faut moins de chiffres en base 10 que dans l'autre base, pour représenter les nombres. Il ne reste plus alors qu'à se limiter aux cases grises qui, elles, contiennent (au moins partiellement) des nombres ayant la même quantité de chiffres dans les deux bases (ce qui les rend éligibles au fait d'être anacycliques)
Résultats
Pour trouver les nombres anacycliques, la meilleure solution consiste à tester un à un chaque nombre dans chaque base (dans les limites définies par le tableau précédent). Cette technique à le mérite d'être fiable et relativement rapide tant que l'on ne doit pas tester des nombres à plus de dix chiffres. En revanche pour les bases 9 11 et 12, le nombre d'éléments à tester est grand voire même, incalculable.
En effet, la limite des nombres que peuvent stocker les machines se situe souvent autour de 2^64 ce qui correspond à un nombre à 22 chiffres. Dans notre cas, il faudra pourtant tester des nombres contenant jusqu'à 25 chiffres, ce qui n'est pas possible. Il existe des manières d'effectuer ces vérifications qui circonviennent à ces problèmes mais les temps de calcul qui en résultent sont encore trop longs.
Bon, en tout cas, la liste est correcte pour toutes les bases sauf pour 9, 11 et 12 donc. Dans ces derniers cas elle sera potentiellement incomplète pour les nombres à plus de 10 chiffres.
Conclusion
On constate aisément que le nombre d'anacycliques est très faible et avec des valeurs extrêmement aléatoires, ce qui incite à conclure que tout ceci est parfaitement inutile et sans aucune application concrète (j'ai beau chercher, je n'y vois strictement aucune utilité).




Aucun commentaire:
Enregistrer un commentaire